Olśniło mnie kiedyś i rozwiązałem takie jedno przykładowe zadanie od A do Z. Postanowiłem wiec zamieścić je dla potomnych bo mi już nie będzie potrzebne. Sesja Zaliczona!!!
Trzy magazyny: M1, M2, M3, zaopatrują w mąkę cztery piekarnie: P1, P2, P3, P4. Jednostkowe koszty transportu ( w zł. za tonę), oferowane miesięczne wielkości dostaw Ai ( w tonach) oraz miesięczne zapotrzebowanie piekarń Bj (w tonach) podano w tabeli poniżej.
Należy opracować plan przewozu mąki z magazynów do piekarń, minimalizujący całkowite koszty transportu.
Oznacza to, że mamy do czynienia zagadnieniem transportowym zamkniętym ( ZTZ)
Zmienne decyzyjne x_ij oznaczają ilość ton mąki, jaka powinna być dostarczona z i-tego magazynu (i=1,2,3) do j-tej piekarni (j=1,2,3,4); jest ich 3*4=12. Ponieważ jest to zagadnienie transportowe zamknięte ( zbilansowane), dostawcy sprzedadzą całą ilość oferowanego towaru, a zapotrzebowania piekarń zostaną w całości zaspokojone.
Ograniczenia dla dostawców
Suma wielkości dostaw mąki z magazynu M do wszystkich piekarń powinna być równa podaży magazynu.
Ograniczenia dla odbiorców
Suma dostaw mąki otrzymanych przez piekarnię P ze wszystkich trzech magazynów powinna być równa całkowitemu jej zapotrzebowaniu.
Minimalizacja łącznych kosztów transportu
Funkcja Celu
Dla tak sformułowanego modelu wyznaczamy początkowe rozwiązanie dopuszczalne ? przykładowo za pomocą dwu wybranych metod.
Metoda kąta północno-zachodniego
Polega na tym, że wypełnienie macierzy przewozów [x_ij ] rozpoczyna się od klatki w lewym górnym rogu ( stąd nazwa kąta północno-zachodniego). Wpisuje się do niej mniejszą z liczb (A_1,B_1) odpowiadających tej klatce, a następnie przesuwa się w prawo lub w dół:
- w prawo, gdy towar pierwszego dostawcy nie został jeszcze całkowicie rozdysponowany,
- w dół, gdy całą podaż tego dostawcy rozdzielono odbiorom.
W rozpatrywanym przykładzie do klatki M_1,P_1 wpisujemy 40 t (x_11=40) i przesuwamy się w prawo
(ponieważ zapotrzebowanie piekarni P_1 zostało zaspokojone, a magazynowi M_1, zostało jeszcze 30t, które dostarczy do piekarni P_2 (x_12=30) . Obecnie przesuwamy się w dół ? do magazynu M_2, który dostarczy brakujące 30t mąki do piekarni P_2 (x_22=30) i pozostałe 20t mąki do piekarni P_3 (x_23=20). Przesuwamy się powtórnie w dół do magazynu M_3, który dostarczy brakujące 30t mąki do piekarni P_3 (x_33=30) i pozostałe 50t mąki do piekarni P_4 (x_34=50).
Rozwiązaniu temu odpowiadają następujące koszty transportu:
Metoda minimalnego elementu macierzy ( klatek zerowych)
Polega na rozmieszczaniu przewozów przede wszystkim po tych trasach, na których koszty są najmniejsze. Punktem wyjścia jest przekształcenie macierzy kosztów do takiej postaci, by w każdym wierszu i w każdej kolumnie występowało, co najmniej jedno zero. Można to uzyskać, odejmując od elementów poszczególnych wierszy macierzy kosztów, najmniejszy element znajdujący się w danym wierszu,
a następnie od poszczególnych kolumn otrzymanej w ten sposób macierzy, odejmując element najmniejszy, znajdujący się w danej kolumnie.
Mając tak przekształconą macierz kosztów, staramy się rozmieścić przewozy na trasy, gdzie koszty są najniższe, czyli gdzie występują zera. Rozmieszczanie przewozów rozpoczynamy od dowolnej klatki zerowej. Jeżeli uda się rozmieścić przewozy wyłącznie w klatkach, w których występują zera, to otrzymane rozwiązanie jest już optymalnym planem przewozów. Jeżeli nie, należy je poprawić stosując algorytm transportowy.
Rozdysponowanie przewozów ( dobrze jest zacząć od tych wierszy lub kolumn w których występuje jedno zero a więc nie mamy wyboru) rozpoczynamy od klatki M_2,P_1 gdzie możemy wpisać tylko 40 ( tyle wynosi zapotrzebowanie P_1) Przechodząc do drugiej kolumny ? do klatki M_3,P_2 wpisujemy 60 , w kolumnie trzeciej wpisujemy 20 na trasę M_3,P_3 i 30 na trasę M_1,P_3. Dla zbilansowania wpisujemy 40 na trasę M_1,P_4 i 10 na trasę M_2,P_4. Ponieważ w tym przypadku udało się rozmieścić wszystkie przewozy w klatkach z zerami ? otrzymane rozwiązanie jest optymalne.
Związane są z nim następujące koszty transportu:
A zatem niższe koszty transportu 8000 zł można osiągnąć nawet gdyby rozwiązanie to nie było jeszcze optymalne ( koszty będą znacznie niższe niż wtedy, gdy rozwiązanie początkowe wyznaczy się metodą kąta północno-zachodniego) . DOTYCZY TYLKO TEGO PRZYPADKU
Solver
Postępować według instrukcji. Analogicznie rozwiązuje się podobne zadania 🙂







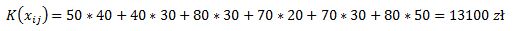




Dzieki wielkie, bardzo mi to pomogło:D
Służę pomocą… 🙂
„Jeżeli uda się rozmieścić przewozy wyłącznie w klatkach, w których występują zera, to otrzymane rozwiązanie jest już optymalnym planem przewozów. Jeżeli nie, należy je poprawić stosując *algorytm transportowy*.”
No właśnie i w moim zadaniu tu się pojawia problem 😐 Ogólnie prezentujesz o wiele prostszą metodę (tą min el macierzy) niż mój profesor wiec mi się spodobała i łatwo ją sobie przyswoiłam jednak nie wiem co dalej :/ Jak wykonać dalej algorytm transportowy? Gdyż kratki z zerami mi sie nie „stykają” :/
Klatki z zerami nie muszą się stykać. Wystarczy, że po uzupełnieniu odpowiednich wartości do klatek zerowych, sumy Ai i Bj będą sobie równe, oraz będą równe wartości z treści zadania.
co jesli prz obliczaniu rozwiazania optymalnego wychodza mi 6 przewozow na minus i 6 przewozow na plus?nie jest wtedy to optymalne? pomimo tego, ze wybieralam najnizsze wartosci z tabeli?
Zaraz, zaraz, jakie przewozy na minus? Nie może być coś na minus… Stosujesz metodę klatek zerowych? Jeśli tak, to nie możesz mieć wartości ujemnych tylko zera.
Aaaa… Dzięki mistrzu! 😀
Badania operacyjne no przyjdź na WAT i zobacz jak to tam wygląda.
Metoda kąta północno-zachodniego, a nie konta
A co zrobić jeśli w zadaniu mam mniej przewozow niz powinnam?
Przecież sami ustalamy ile ma być przewozów.
Chyba chodzi o przypadek gdy nie jest zachowany bilans i mamy np. 3 magazyny i 3 dostawców.
Dzień dobry,
co w przypadku gdy mamy blokadę trasy, np. M2 do P1 jest nie przejezdna, wiem, że musimy wtedy wstawić wartość trzy krotnie większą niż największa wartość w tabeli, ale w którym momencie trzeba to uczynić, na którym etapie zadania i jak wtedy przebiegnie zadanie?
Z góry dziękuję za odpowiedź
Ja nie wiem, ktoś inny może pomóc?
Jak policzyc jednostkowe koszty transportu nie wiem skad sa dane w srodku tabeli??
Te dane są podane w treści zadania. Ich się nie oblicza. (raczej)
Sasni – mogę prosić Twojego maila, bo mam pytanie odnośnie tego zadania. (mój email: golda.karolcia@interia.pl)
Proszę napisać w wątku, może inni też mają pytania to się wyjaśni…
dzięki akurat z tego mam sprawdzian 😀
Witam,
Jak sprawdzić optymalność rozwiązania które otrzymałeś tj. 8000 tyś.? Jeden egzamin już oblałem, tabela rozwiązana dobrze ale dr wytknęła mi, że od razu uznałem je za optymalne i nie sprawdziłem optymalności. Jak to zrobić.
Pozdrawiam
Wprowadzamy dodatkowe zmienne, tzw. potencjały:
dostawców ui, i=1,…,N
dla odbiorców vj, j=1,…,M
Dla zmiennych bazowych rozwiązujemy układ równań ui + vj + cij=0, przyjmując dla jednego z potencjałów wartość 0.
Wyznaczamy wartości wskaźników optymalności ui + vj + cij dla zmiennych niebazowych.
Jeżeli wszystkie wskaźniki optymalności dla zmiennych niebazowych są dodatnie, to aktualne BRD jest optymalne (koniec algorytmu).
Jeśli nie, to wyznaczamy następne, lepsze BRD, wymieniając jedną ze zmiennych bazowych.
http://www.tarapata.strefa.pl/p_ekonometria/download/ekonometria_cz3_4.pdf tutaj jest to ekstra opisane
mam to w technikum a nauczycielka tak dennie to opisała jakaby sama nie wiedziała o co chodzi tu przynajmniej wszystko z grubsza jasne
Dlaczego przypisujesz sobie „rozwiązanie” tego przykładu, jeśli zarówno zadanie, cały tekst który tutaj wpisałeś i rozwiązanie jest żywcem przepisane z książki K.Kukuła, J. Skrzypek pt.” Badania operacyjne w przykładach i zadaniach”.
Żałosne….
Studia skończyłem już dobre kilka lat temu, przytoczonej książki nie miałem nigdy w ręku. Jest jednak prawdopodobne, że prowadzący zajęcia wykorzystał tenże przykład na ćwiczeniach/wykładzie. Nie mówię, że nie, natomiast trudno jest weryfikować, jak i skąd prowadzący gromadzi materiały na zajęcia. Proszę więc o weryfikację, czy przytoczony przykład jest przepisany „żywcem” czyli słowo w słowo, czy tylko rozwiązałem poprawnie zadanie opisując to swoimi słowami. Bo chyba nie będziesz mieć do mnie pretensji, że udało mi się poprawnie rozwiązać przykład…
Sasni ~ To je cebula, tego nie zasiejesz :D. Życzę wytrwałości w prowadzeniu strony, przyda się przy takich jak p. Daniel
Przydatny wpis
Witam, co jezeli Bj nie rowna sie Ai? I drugie co jezeli mam dodatkowy warunek jak cena do kazdego magazynu?
Prosze o pomoc…
Świetne rozwiązanie, cieszę się że ktoś poświęcił czas i to jasno wyjaśnił. Pozdrawiam